なぜ、”ｎ角形の外角の和は360°”なのか？を説明します

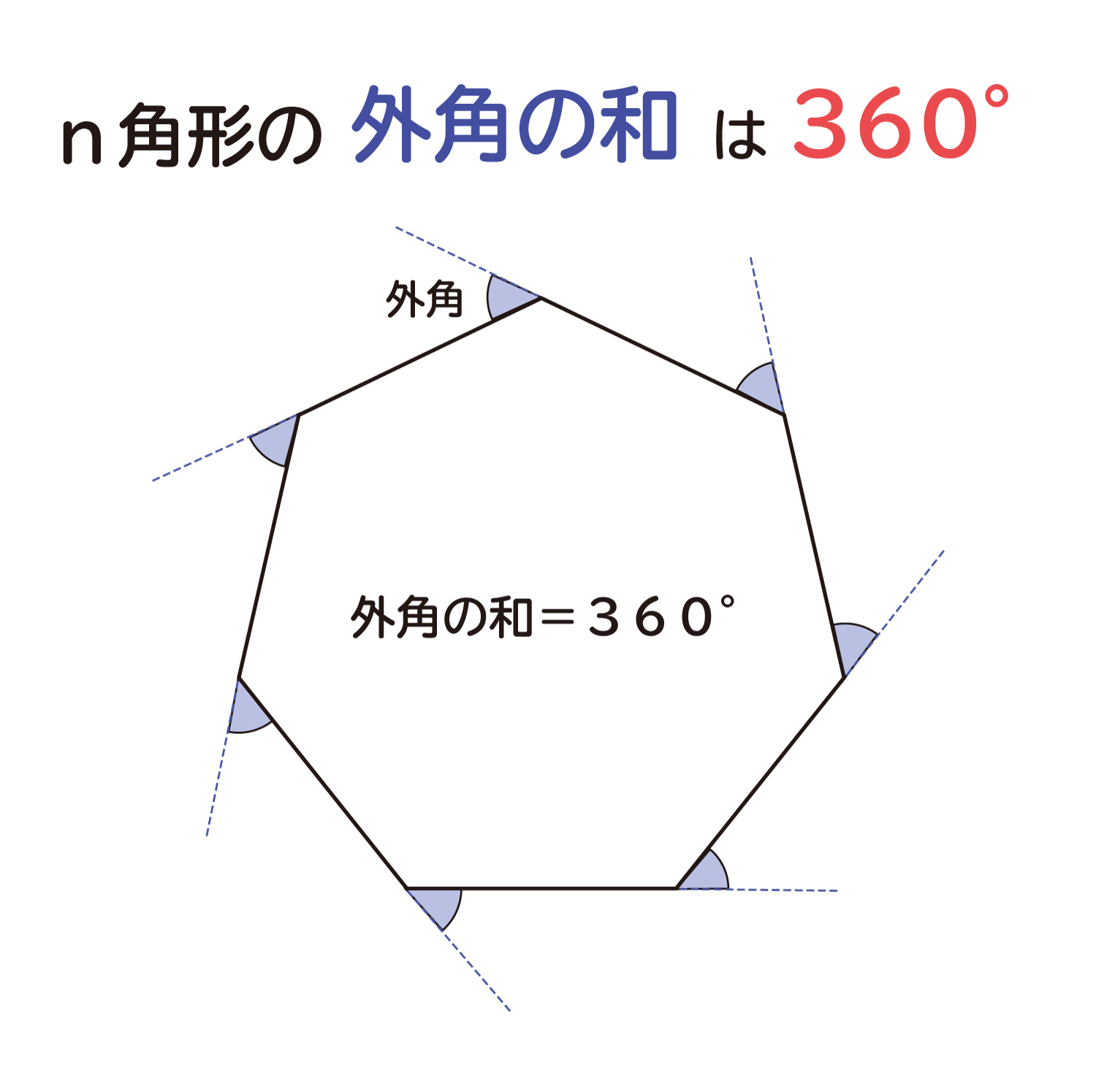
なぜ、”ｎ角形の外角の和は360°”なのか？の説明図１ここでは、なぜ「ｎ角形の外角の和は３６０°」になるのか？を確認していきたいと思います。

この公式のポイント

・ｎ角形は、ｎがいくつのときも外角の和は３６０°になります。

・この公式を理解するためには、ｎ角形の内角の和は１８０°×（ｎ－２）という公式を使います。

ぴよ校長

ｎ角形の内角の和の公式は覚えているかな！？

この公式を理解するために、ｎ角形の内角の和の公式を使います。もし忘れてしまった時は、先に下のリンクから確認してみて下さいね。

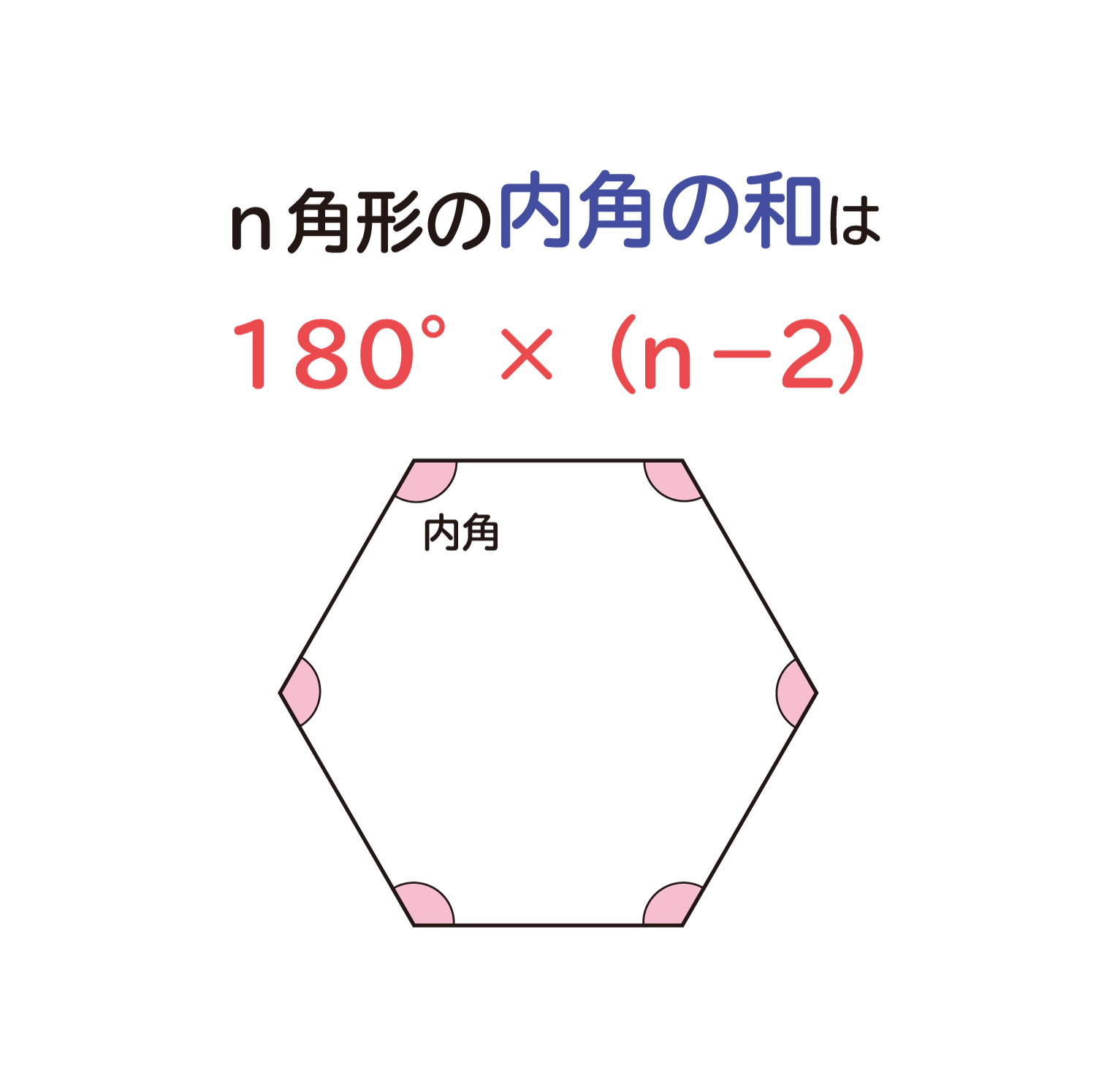
: 「ｎ角形の内角の和は、" １８０°×（ｎ－２）”」になる説明

ここではなぜ、ｎ角形の内角の和は「１８０°×（ｎ－２）」で求めることができるのか？を確認していきたいと思います。この公式のポイント・ｎ角 ...

続きを見る

ぴよ校長

さっそく、ｎ角形の外角の和の公式を確認していこう！

「ｎ角形の外角の和は３６０°」になる説明

下の図のような多角形を考えた時、それぞれの頂点から辺の延長線を引くと、外角を作ることが出来ます。そして、それぞれの頂点で外角と内角の和は１８０°（直線）になっていることが分かります。ｎ角形では頂点がｎ個あるので、ｎ角形の全ての外角と内角の和は「１８０°×ｎ」になっています。

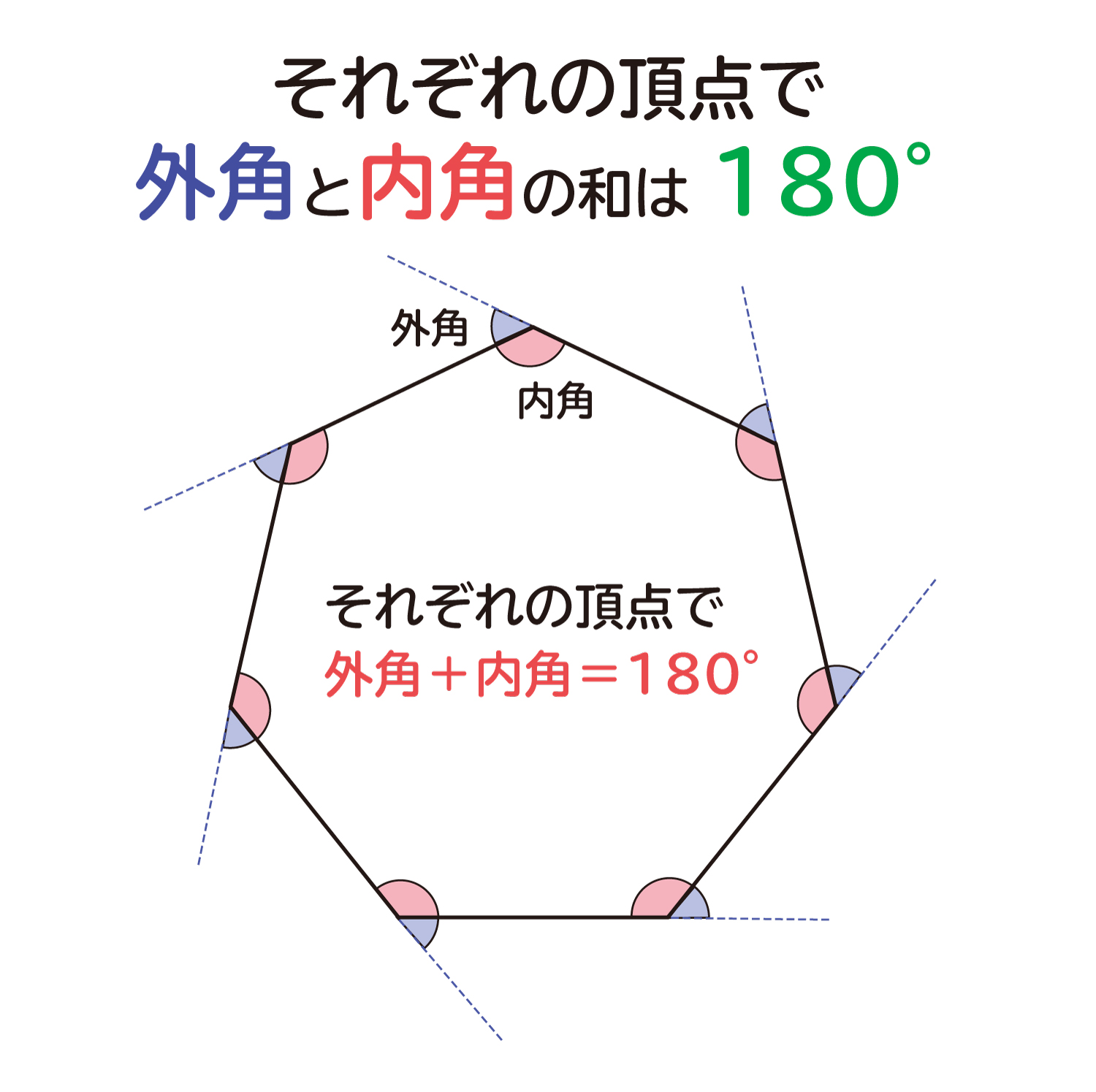
なぜ、”ｎ角形の外角の和は360°”なのか？の説明図２

ｎ角形の外角の和を求めるために、ここからｎ角形の内角の和である１８０°×（ｎ－２）を引いてみましょう。

ｎ角形の外角の和＝１８０°×ｎ－１８０°×（ｎ－２）＝３６０°

ぴよ校長

これでｎ角形の外角の和を求めることができたね！

まとめ

・ｎ角形のそれぞれの頂点の外角と内角の和は１８０°（直線）になっています。

・全ての頂点の外角と内角の和「１８０°×ｎ」から、ｎ角形の内角の和である１８０°×（ｎ－２）を引くと、外角の和として３６０°を求めることが出来ます。

ぴよ校長

ｎ角形の外角の和の公式を覚えることが出来たかな！

「中学2年生の公式の解説」一覧