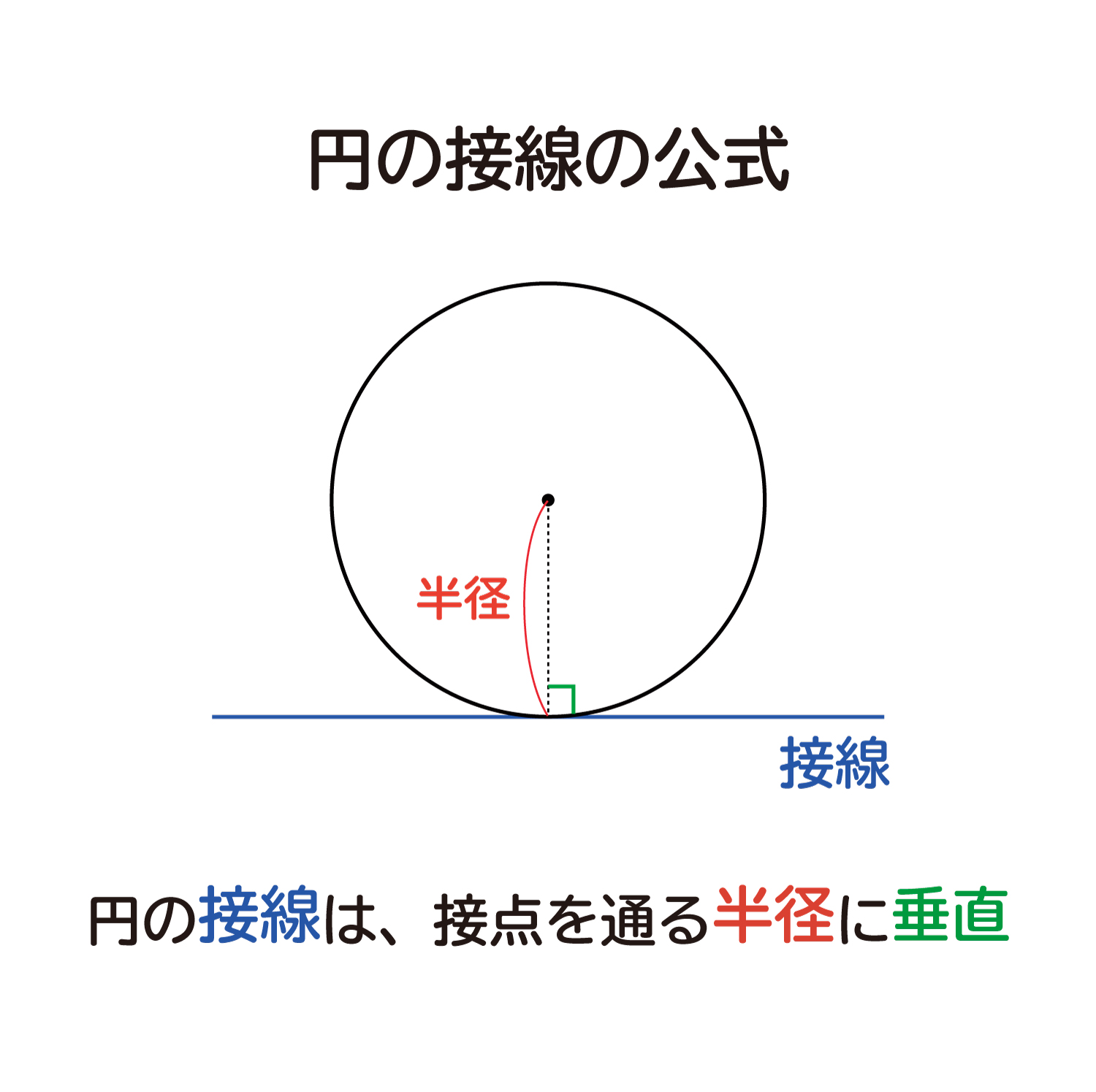
ここでは、なぜ「円の接線は、接点を通る半径に垂直」なのか?を、考えていきます。
この公式のポイント
・円の接線は、その接点を通る半径に垂直になります。

ぴよ校長
教科書に出てくるこの公式が、なぜ成り立つのか確認して納得してみよう!
中学1年生では、円と直線の関係としてこの公式が出てきます。
ここでは図を使って、なぜこの公式が成り立つのか?を考えながら、理解していきたいと思います。

ぴよ校長
それでは円の接線の公式を確認してみよう!
「円の接線は、接点を通る半径に垂直」になる説明
まずは、下の図のように円と2点で交わる直線を引いて、円と直線の交点を点A、点Bとします。
円の中心を点O、直線ABの中点を点Mとします。
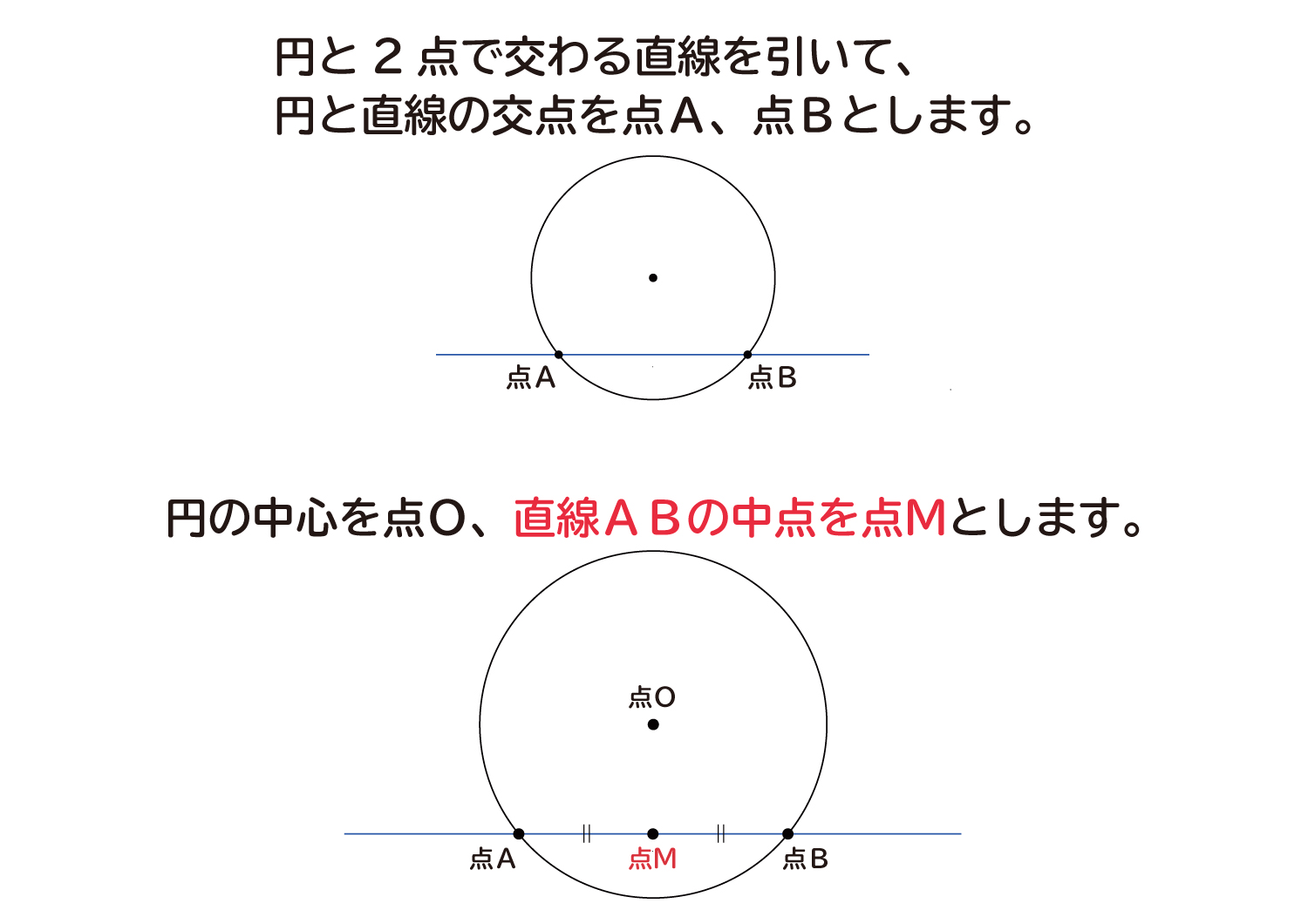
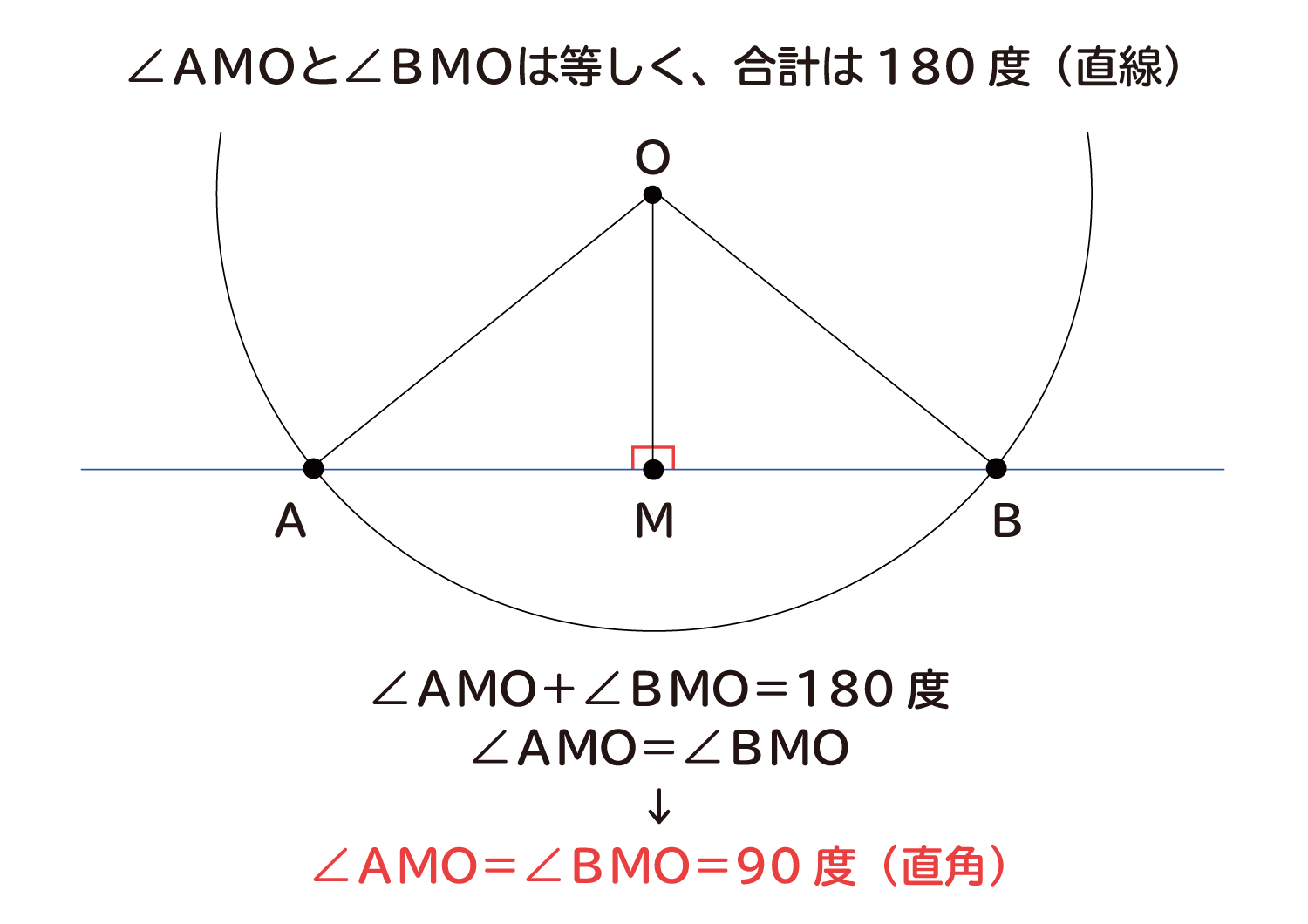
ここで、三角形AMOと三角形BMOは、3辺の長さが全て同じなので、合同な三角形になっています。△AMO≡△BMO

合同な三角形は、全ての角が等しいので、∠AMOと∠BMOは等しくなります。
∠AMOと∠BMOの角度の合計は180度(直線)なので、∠AMO=∠BMO=90度(直角)になり、直線ABに対して直線MOは垂直になっているとわかります。
直線ABを円の中心から外側に移動させていき、直線が円の円周と重なった接線になったとき、直線MOは半径と同じになり、接線と半径は垂直になっています。
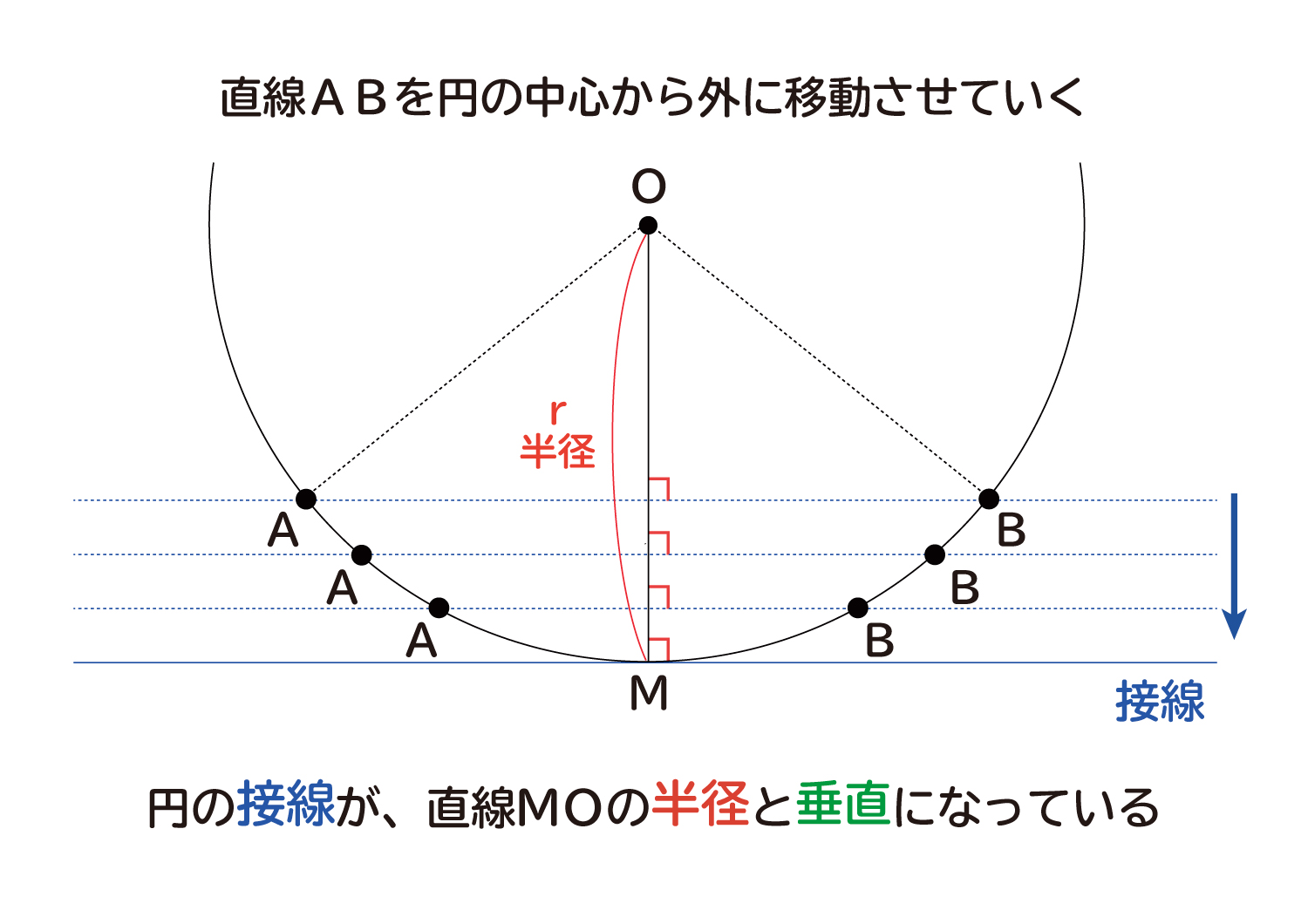
これで、「円の接線は、その接点を通る半径と垂直になる」という公式が確認できました。

まとめ
・円に交わる直線は、その中点と円の中心を通る直線と、垂直に交わります。
・円に接する直線は、接点を通る円の半径と垂直に交わります。

ぴよ校長
円に接する直線と、半径の公式を説明してみたよ
