ここでは、なぜ比例式「a:b=c:d」は「ad=bc」に書き換えられるのか?を、考えていきます。
この公式のポイント
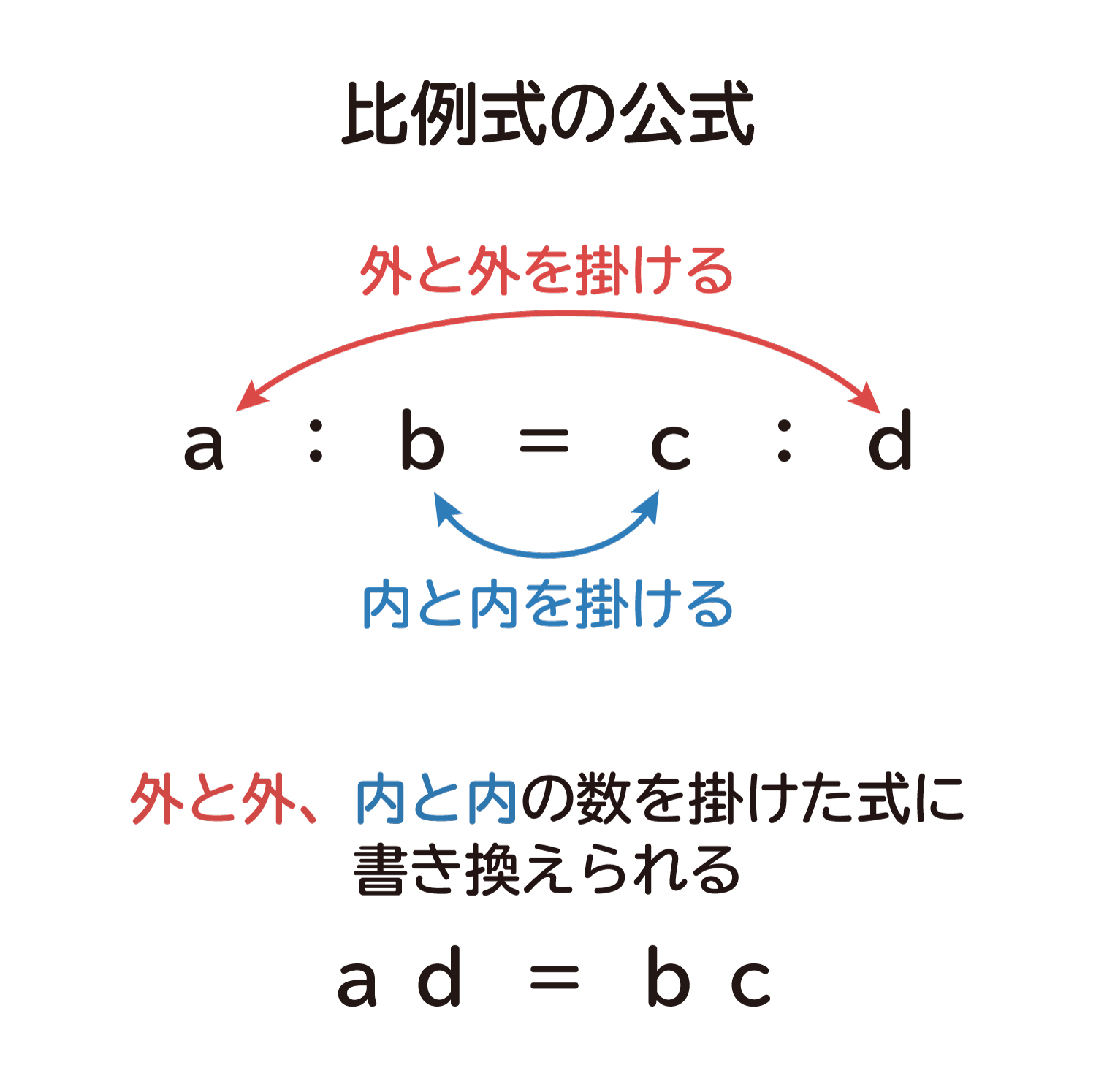
・a:b=c:d なら ad=bc と書き換えることができます。
・比例式の外と外、内と内の数を掛けて書き換えます。

ぴよ校長
比例式で掛ける数は「外(そと)と外(そと)」「内(うち)と内(うち)」と掛けるよ
比例式は、なぜこの公式で書き替えられるのか?を考えながら、理解していきたいと思います。
中学1年生の一次方程式では、この比例式の公式を使って解く問題も出てきます。ぜひ、比例式の公式の考え方を確認してみて下さい。

ぴよ校長
それでは比例式の公式を確認していこう!
「a:b=c:d」は「ad=bc」に書き換えられる説明
「a:b」の比があるとき、比は「比の値 a/b」へ書き換えることができます。
比の値とは、「a」が「b」の何倍かを表す分数のことです。

ぴよ校長
まずは比例式「a:b」を、比の値「a/b」に書き換えてみよう!
$$\Large{a}:{b}$$
$$\Large\frac{a}{b}$$
比が等しいとき、その「比の値」も等しくなるので、比例式は次のように書き換えることができます。
$$\Large{a}:{b} ={c}:{d} $$
$$\Large\frac{a}{b}=\frac{c}{d}$$
次に「比の値」を整数に変えるために、両辺に「b×d」を掛けます。
$$\Large\frac{a}{b}=\frac{c}{d}$$
$$\Large\frac{a}{b}×{b}×{d}=\frac{c}{d}×{b}×{d}$$
$$\Large{a}{d}={b}{c}$$

ぴよ校長
「a:b=c:d」が「ad=bc」に書き換わったね!
まとめ
・比例式「a:b=c:d」を、比の値「a/b=c/d」に書き換えます。
・次に、比の値を整数に書き変えると「ad=bc」になります。

ぴよ校長
これで、比例式の公式も大丈夫だね!
