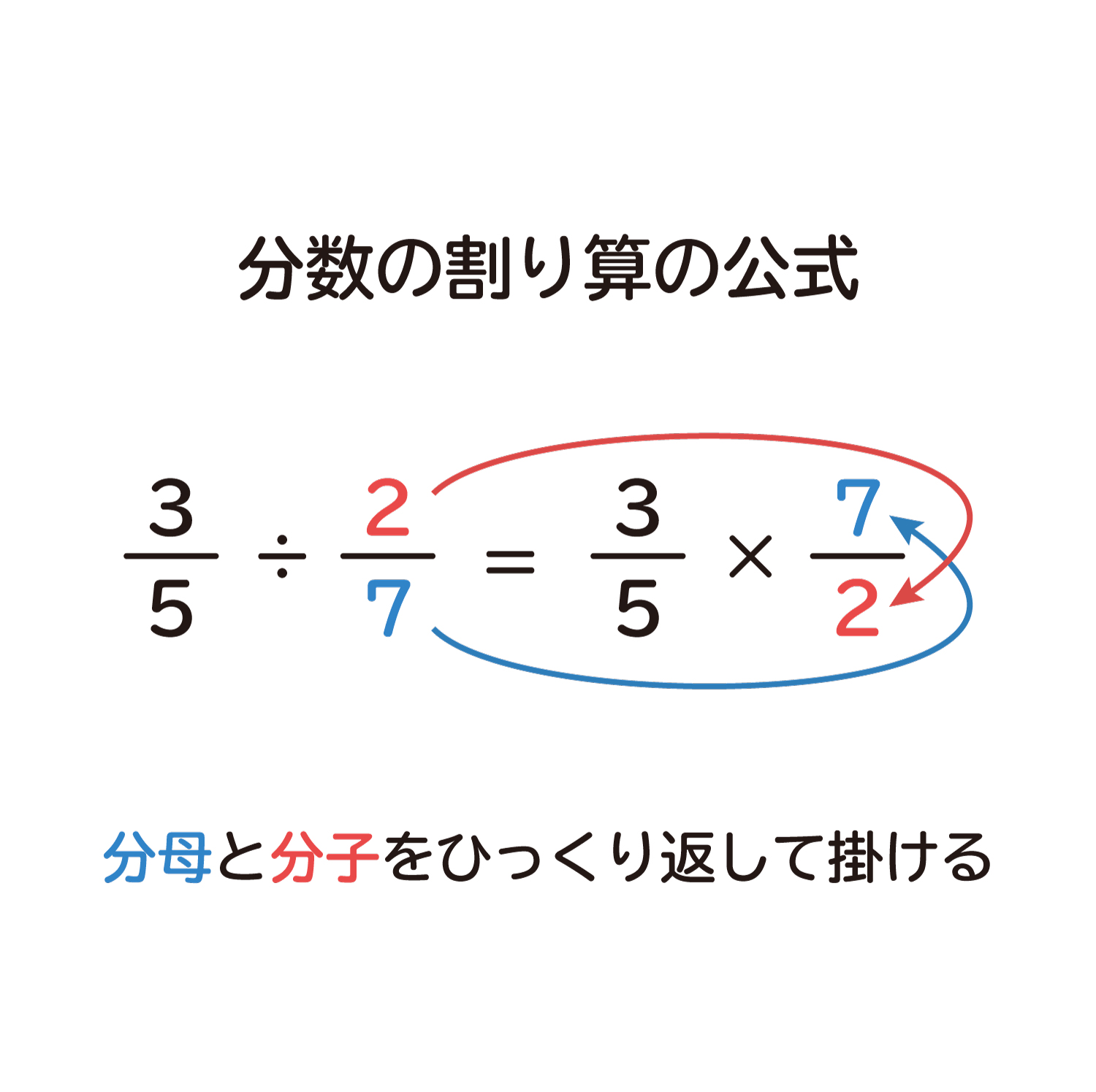
ここでは、なぜ分数の割り算は「分母と分子をひっくり返して掛ける」のか？を、考えていきます。
この公式のポイント
・分数の割り算は、分母と分子をひっくり返して掛けます。
分数の割り算は、なぜこの公式で求められるのか？を考えながら、理解していきたいと思います。
なぜひっくり返して掛けるのかは、小学生が疑問に思うことも多い公式です。大人も子どもから聞かれたときに、説明しにくい公式かもしれません。
ぜひ、分数の割り算の考え方を確認してみて下さい。
今回は、分数の割り算の公式を理解するための、２つの考え方を紹介したいと思います。自分で納得しやすい方の考え方で、ぜひこの公式を覚えてみて下さい。
分数の割り算は「分母と分子をひっくり返りして掛ける」説明～その①～
まず１つ目の考え方は、割り算の計算は「割られる数」と「割る数」のそれぞれに同じ数を掛けて計算しても、答えは変わらないという性質を使います。
例えば、下のような割り算を考えます。
$$\Large{8}\div{4} ={2}$$
この時、「割られる数の８」と「割る数の４」のそれぞれに、同じ「１０」を掛けて計算してみます。
$$\Large{(8×10)}\div{(4×10)}$$
$$\Large={80}\div{40}$$
$$\Large={2}$$
上の計算ように、割り算は「割られる数」と「割る数」のそれぞれに、同じ数字を掛けて計算しても答えが変わらない性質を持っています。これを分数の割り算にも応用することで、分数の割り算が計算できます。
次は実際に、下のような分数の割り算を考えてみます。
$$\Large\frac{3}{5}\div\frac{2}{7} $$
この割り算で、「割られる数」と「割る数」のそれぞれに同じ数を掛けます。この時に掛ける数は
「割る数の逆数」である7/2を掛けてみます。
$$\Large\frac{3}{5}\div\frac{2}{7} =(\frac{3}{5}×\frac{7}{2})\div(\frac{2}{7}×\frac{7}{2} )$$
そうすると、割る数は１になり、下のように計算することができます。
$$\Large\frac{3}{5}\div\frac{2}{7}=(\frac{3}{5}×\frac{7}{2})\div(\frac{2}{7}×\frac{7}{2})$$
$$\Large=(\frac{3}{5}×\frac{7}{2})\div{1}$$
$$\Large=\frac{3}{5}×\frac{7}{2}$$
では、もう１つの考え方も見てみましょう。
分数の割り算は「分母と分子をひっくり返りして掛ける」説明～その②～
先ほどの考え方とは少し違う、もう１つの考え方を下で紹介します。
分数の割り算を理解する為に、まずは分数をアルファベットの文字にした計算を考えてみます。
$$\Large{a}\div{b} =\frac{a}{b}$$
次にこのアルファベットに、例えばそれぞれ下のような分数の数を入れてみましょう。
$$\Large{a}=\frac{3}{5}$$
$$\Large{b}=\frac{2}{7}$$
ａとｂに、上の分数を入れてみた場合、下のような計算になります。
$$\Large{a}\div{b} =\frac{a}{b}$$
$$\Large\frac{3}{5}\div\frac{2}{7}=\frac{\frac{3}{5}}{\frac{2}{7}} $$
この分数の分数を、簡単な形にするために「分母の逆数」を分母と分子の両方に掛けて、分母を「１」にします。
$$\Large\frac{\frac{3}{5}}{\frac{2}{7}}= \frac{\frac{3}{5}×\frac{7}{2}}{\frac{2}{7}×\frac{7}{2}}$$
$$\Large=\frac{\frac{3}{5}×\frac{7}{2}}{1}$$
$$\Large=\frac{3}{5}×\frac{7}{2}$$
まとめ
・考え方①：「割られる数」と「割る数」のそれぞれに、「割る数の逆数」を掛けるという考え
・考え方②：分数の割り算を、分数の分数の形に変えるという考え
その他の小学生の算数の解説は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さい。