ここでは、中学3年生で習う多項式の展開公式について説明をしていきたいと思います。
多項式の展開では、式の形によってさまざまな展開公式があります。
ここでは、「いろいろな多項式の展開公式」について、計算しながら、なぜこのような式の形になるかを確認していきたいと思います。
この公式のポイント
・多項式の展開公式は、下のような４つの公式があります。
$$\Large公式１ (x+a)(x+b)=x^2+(a+b)x+ab$$
$$\Large公式２ (x+a)^2=x^2+2ax+a^2$$
$$\Large公式３ (x-a)^2=x^2-2ax+a^2$$
$$\Large公式４ (x+a)(x-a)=x^2-a^2$$
中学3年生で習う多項式の展開公式は上の４つになります。今回はこの４つの展開公式を、それぞれどのように計算して、このような形の式になっているのかを確認していきましょう。
多項式の展開方法を考えるときは、分配法則の考え方が必要になります。多項式を分配法則を使って展開する方法について、もし忘れてしまった場合には、下のリンクに説明を書いているので、先にぜひ確認してみて下さいね。
-
-
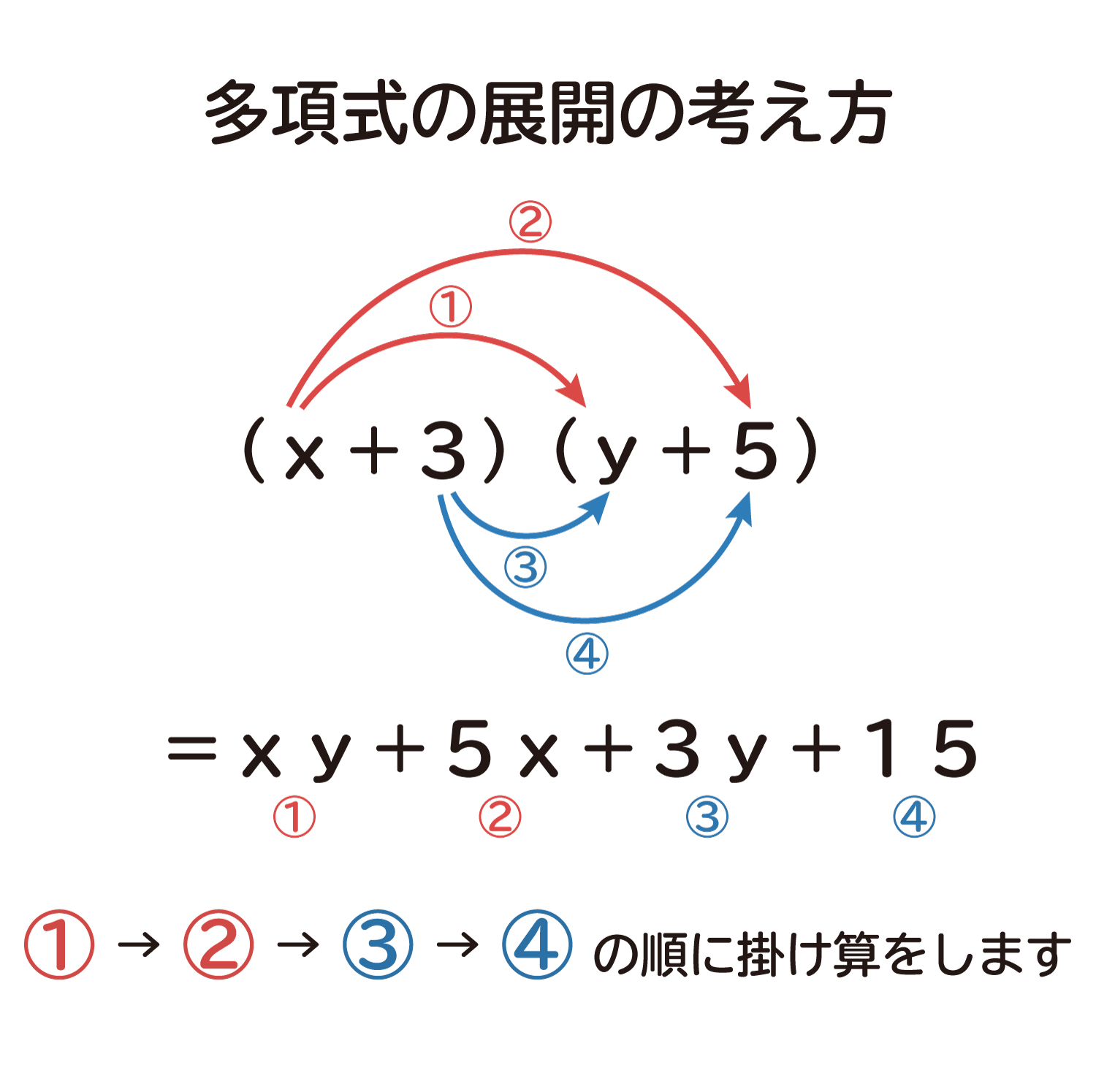
多項式同士の掛け算の展開の考え方
ここでは、多項式同士の掛け算の展開の考え方を説明していきたいと思います。 中学校では、多項式の展開の公式がいくつか出てきますが、今回は展開公 ...
続きを見る
「多項式の展開公式」についての説明
多項式の展開公式を、公式１から確認していきたいと思います。
$$\Large公式１ (x+a)(x+b)=x^2+(a+b)x+ab$$
この式の左辺は、展開すると下のよう計算することができます。
$$\Large(x+a)(x+b)=x^2+bx+ax+ab$$
$$\Large=x^2+(a+b)x+ab$$
以上で展開公式１を確認できました。
続いて、公式２を確認していきます。
$$\Large公式２ (x+a)^2=x^2+2ax+a^2$$
この式の左辺は、展開すると下のようになります。
$$\Large(x+a)^2=x^2+ax+ax+a^2$$
$$\Large=x^2+2ax+a^2$$
同じように、公式３も確認していきます。
$$\Large公式３ (x-a)^2=x^2-2ax+a^2$$
この式の左辺は、展開すると下のようになります。
$$\Large(x+a)^2=x^2-ax-ax+a^2$$
$$\Large=x^2-2ax+a^2$$
最後に、公式４を確認します。
$$\Large公式４ (x+a)(x-a)=x^2-a^2$$
この式の左辺は、展開すると下のようになります。
$$\Large(x+a)(x-a)=x^2-ax+ax-a^2$$
$$\Large=x^2-a^2$$
まとめ
・多項式の展開公式は、分配法則を使った計算で確認できます。
その他の中学生で習う公式は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さいね。